在单轴拉伸流动中测量了三种选定的商用低密度聚乙烯(LDPE)的非线性流变性能。使用三种不同的设备进行测量,包括拉伸粘度装置(EVF),自制长丝拉伸流变仪(DTU-FSR)和商用长丝拉伸流变仪(VADER-1000)。通过测试显示,EVF的测量结果受到最大Hencky应变4的限制,而两个长丝拉伸流变仪能够在达到稳态的更大Hencky应变值下探测非线性行为。利用长丝拉伸流变仪的能力,我们表明具有明显差异的线性粘弹性的低密度聚乙烯可以具有非常相似的稳定拉伸粘度。这表明有可能在一定的速率范围内独立控制剪切和拉伸流变。
拉伸流变;聚乙烯;聚合物熔体;非线性粘弹性
多年来,控制聚合物流体的流变行为作为分子化学的一个性能,引起了学术界和工业界的极大兴趣。
最成功和最多产的理论预测的流变行为的纠缠聚合物系统是De Gennes(1971)和Doi和Edwards(1986)提出的 "管模型"。然而,尽管三十年来人们一直在努力改进管模型,但即使对于最简单的情况,即单分散线性聚合物体系,缠结聚合物在拉伸流动中的非线性流变行为仍然没有得到充分理解(Huang等人,2013a;Huang等人,2013b)。低密度聚乙烯等工业聚合物是最复杂的缠结聚合物系统,它们不仅具有高度的多分散性,而且还含有不同的支化分子结构。预测低密度聚乙烯的流变行为,特别是拉伸流动中的非线性行为,是非常具有挑战性的。
在明确定义的模型系统上,已经进行了探索延伸流中支化聚合物动力学的实验工作(Nielsen等人,2006;Van Ruymbeke等人,2010;Lentzakis等人,2013)以及商业聚合物系统,如低密度聚乙烯LDPEs。
有几个小组观察到低密度聚乙烯LDPE的瞬时拉伸应力的最大值(Raible等人,1979;Meissner等人,1981;M¨unstedt和Laun,1981)。Rasmussen等人(2005年)首次报告了应力过冲后的稳定应力,并通过比较长丝拉伸流变仪和十字槽拉伸流变仪的测量结果(Hoyle等人,2013年)以及比较恒定拉伸速率和恒定应力(蠕变)实验(Alvarez等人,2013年)进行了实验验证。
已经开发了几个模型(Hoyle等人,2013;Wagner等人,1979;Hawke等人,2015),试图了解应力过冲背后的物理学。然而,这些模型都不能实际用于预测工业中低密度聚乙烯LDPE的流变行为,因为这些模型包含许多与分子结构没有直接关系的拟合参数。
最近,Read等人(2011)提出了一个预测方案,能够计算随机长链支化聚合物熔体的线性和非线性粘弹性,作为其形成的化学动力学的函数。这些预测似乎与剪切流和拉伸流中三个低密度聚乙烯的测量结果非常一致。然而,测得的拉伸数据受到最大Hencky应变约为3.5的限制,并且没有显示出稳定状态的迹象,而模拟结果则达到了更大的 Hencky应变值,并预测了每个应变速率的稳定应力。在更大的Hencky应变值下预测非线性行为的质量仍然是未知的。此外,在Read等人(2011)的模拟中,没有预测到应力过冲。
在这项工作中,我们介绍了三种不同的商用低密度聚乙烯的拉伸测量。这三种低密度聚乙烯是根据Read等人(2011)的模型预测而专门设计的。预计它们具有不同的零剪切速率粘度,但在非线性拉伸流动的大变形中具有相似的应力-应变反应。测量是在三个不同的设备上进行的,包括两个长丝拉伸流变仪和一个拉伸粘度夹具。我们表明,长丝拉伸流变仪的测量结果可以达到5以上的大Hencky应变值,在那里达到非线性稳定状态。我们还表明,低密度聚乙烯LDPE样品在拉伸流动中的大Hencky应变值具有相似的非线性行为,包括相同的应力过冲幅度和过冲后的相同稳定应力,尽管Read模型预测没有应力过冲现象。这些结果表明,低密度聚乙烯LDPE熔体的非线性粘弹性可以通过选择性聚合方案来控制。
材料
陶氏化学公司提供了三种类型的商用低密度聚乙烯树脂,分别为PE-A、PE-B和PE-C。所有样品都是颗粒状的。表1总结了样品的特性,包括密度、熔体流动指数(I2)、重量-平均摩尔质量(Mw)、数量-平均摩尔质量(Mn)和熔体强度。重量-平均摩尔质量是由多角度激光散射法确定的,而数量-平均摩尔质量是由微分折射率确定的。摩尔质量值是若干次重复的平均数。熔体强度是用通用流变仪结合通用ALR-MBR 71.92挤出机测量的。测量是在150℃下进行的,产量为600g/h。模具的长度为30毫米,直径为2.5毫米。

实验是在24mm/s2的加速度下进行的。纺丝线的长度被设定为100毫米。流变仪测试在膜生物反应器挤出机系统清扫30分钟后进行,并一直运行到纺丝线失效。通过力-拉速数据拟合出一个四参数交叉函数,根据拟合的破坏速度曲线确定破坏时的力。表中的数据是五次连续测量的平均数。
力学谱
三种低密度聚乙烯样品的线性粘弹性(LVE)特性是通过小振幅振荡剪切(SAOS)测量得到的。TA仪器公司的ARES-G2流变仪采用25毫米的板-板几何形状。
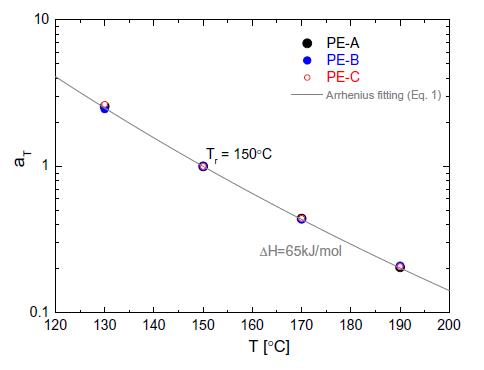
图1所有样品的时间-温度偏移因子αT作为温度的函数,参考温度为Tr= 150℃
测量是在氮气中,在130℃和190℃之间的不同温度下进行的。对于每个样品,使用时间-温度叠加(TTS)程序,在参考温度Tr= 150℃时,数据被移动到单个主曲线。所有样品的时间-温度偏移系数(αT)与单一的阿伦尼乌斯公式一致,其形式为
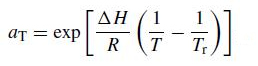
其中活化能∆H = 65 kJ/mol。R是气体常数,T是以开尔文表示的温度。在图1中,偏移因子αT被绘制为温度的函数。
拉伸应力测量
拉伸应力测量使用三种不同的设备:TA仪器的延伸粘度夹具(EVF)、自制的长丝拉伸流变仪(DTU-FSR)(Bach等人,2003a)和Rheo Filament的商用长丝拉伸流变仪(VADER-1000)。将不同设备的结果进行相互比较。
用于EVF测量的样品在150℃下压缩成型,在低压10bar下3分钟,在高压150bar下1分钟,然后用淬火冷却盒在150bar下淬火冷却到室温。在短时间内,当冷却盒插入时,样品会出现压力损失。在相对较低的温度下进行短时间的压缩成型是为了防止样品的任何潜在氧化或降解。样品模具为特氟隆涂层,尺寸为100×100 0.5mm。从约20mm长的铭牌上冲压出12.7mm-12.8mm宽的样品。最终样品的厚度约为0.6mm。在EVF测量中,样品被插入设备中,在150℃下180s的平衡时间后,样品以0.005s-1的应变速率被预拉伸15.44s,然后松弛80s,然后样品被拉伸。报告的Hencky应变是由圆柱体的旋转计算出来的。
通常情况下,使用EVF的拉伸测量仅限于样品保持均匀的情况。EVF一次旋转所能达到的Hencky应变值通常低于4,与EVF相比,长丝拉伸仪器并不依赖于沿拉伸方向的均匀变形的假设。事实上,由于板材上的无滑移条件,变形在轴向上是不均匀的。这些设备只是探测了通常在中间细丝平面发现的最小直径平面内的变形和应力之间的关系。在这个平面外的剩余材料只需要固定在研究的薄片上,就像在固体力学测试中用狗骨形状来固定材料一样。长丝拉伸装置确实依赖于最小直径平面内的径向均匀变形的假设。Kolte等人(1997年)的模拟表明,在长丝中间平面几乎没有任何径向应力变化。用激光测微计来测量中丝薄片的直径。为了探索更高的应变,在DTU-FSR和VADER 1000流变仪都采用了在线控制方案,该方案首先由Bach等人(2003b)使用,后来由Mar´ın等人(2013)发表,用于在拉伸过程中控制长丝中平面的直径,以便在样品断裂前确保恒定的应变速率。根据样品的类型,DTU-FSR和VADER-1000都可以达到最大Hencky应变值7。
在长丝拉伸流变仪上进行测量之前,样品被热压成半径为R0、长度为L0的圆柱形试样。长宽比定义为∆0= L0/R0。样品在150℃下压制,并在相同温度下退火10分钟,然后冷却至室温。在测量中,所有样品被加热到150℃,在180s的平衡时间后,样品在拉伸实验之前被预拉伸到Rp的半径。对于DTU-FSR,R0= 4.5mm,L0= 2.5mm,Rp在3到4.5mm之间,而对于VADER-1000,R0 = 3.0mm,L0= 1.5mm,Rp = 2.5mm。在拉伸测量过程中,力F(t)由称重传感器测量,中间灯丝平面的直径2R(t)由激光测微计测量。在拉伸流动开始的小变形时,由于变形场中的剪切分量,部分应力差来自于压力的径向变化。这种影响可以通过Rasmussen等人(2010)描述的校正因子来补偿。 对于大应变,校正消失,对称平面中应力的径向变化变得可以忽略不计(Kolte等人,1997)。对于本工作中的所有样本,当Hencky应变值大于2时,校正值小于4 %,Hencky应变和中丝平面上应力差的平均值计算如下
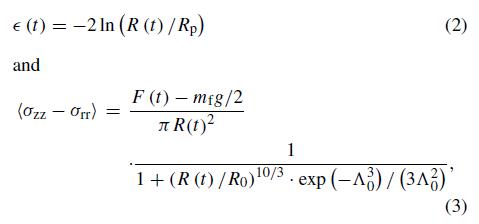
其中mf是灯丝的重量,g是重力加速度。应变率定义为ϵ•=dϵ/dt,拉伸应力增长系数定义为η-+=〈σzz-σrr 〉/ϵ•
线性粘弹性
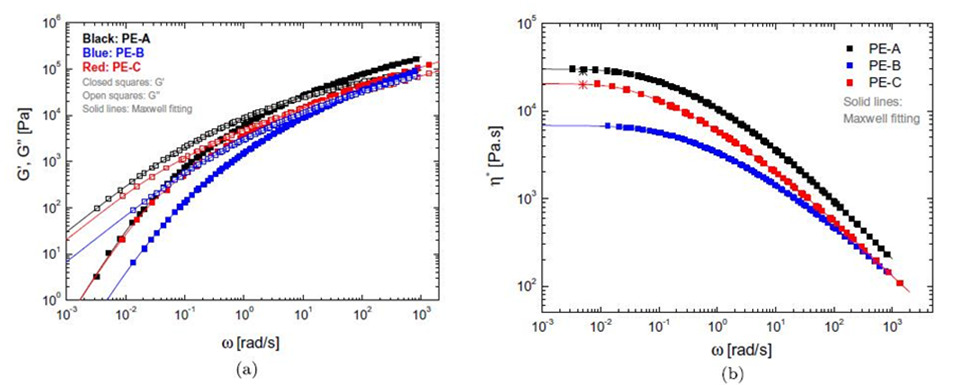
图2(a)显示了所有样品在参考温度150℃下的储能模量G’和损耗模量G”与角频率ω的函数关系。(b)表示在150°C相应的复数粘度η*。图中的两个星号来自稳定剪切测量,在 150°C下剪切速率为0.005 s-1
图2(a)显示了所有样品在参考温度150℃下的储能模量G’和损耗模量G”与角频率ω的函数关系。相应的复数粘度η*绘制在图2(b)中。图中实线是多模麦克斯韦(multimode Maxwell fitting)拟合的结果。Maxwell relaxation modulus多模麦克斯韦弛豫模量G(t)由下式给出
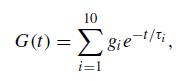
其中gi和τi列于表2。表中的零剪切速率粘度η0通过下式计算
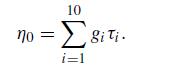
在图2(b)中,很明显三个样品具有不同的零剪切速率粘度。然而,在图2(a)、(b)中,似乎PE-C的线性行为在较低频率下接近PE-A,在较高频率下与PE-B重叠。而且在ω> 1 rad/s时,PE-C的G′和G〃曲线几乎与PE-A平行,垂直位移因子约为0.6。
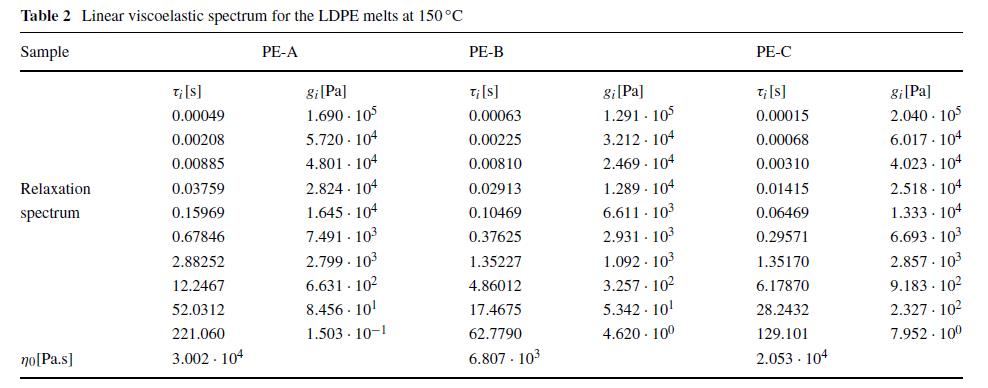
表2 LDPE 在 150°C 熔体的线性粘弹性
启动和稳定状态下的拉伸流变
图3(a)显示了PE-A在150℃时的拉伸应力增长系数与时间的关系。图中比较了EVF、DTU-FSR和VADER-1000的测量值。图中的虚线是根据表2中列出的麦克斯韦弛豫谱计算的LVE包络线。EVF的测量值受到最大Hencky应变4的限制,在图3(b)中可以清楚地看到。其中测量的应力是作为Hencky应变的函数绘制的。两个长丝拉伸流变仪的测量值能够达到大于5的较大Hencky应变值,在该值下观察到稳定的应力。
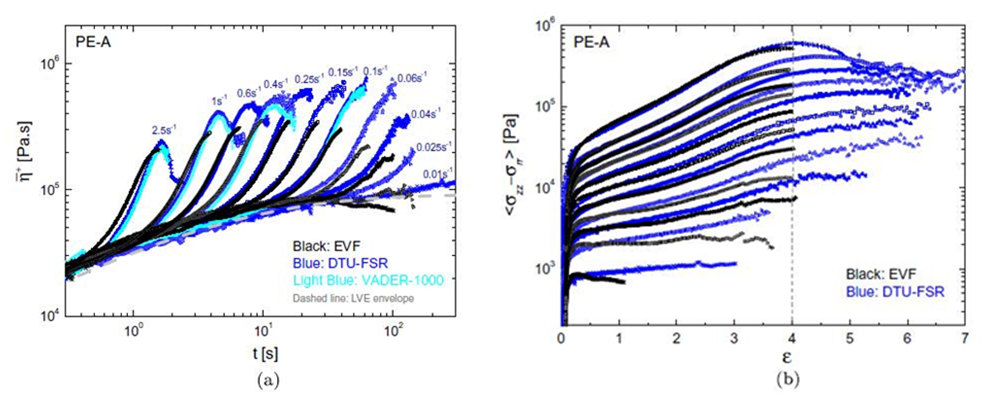
图3
我们注意到EVF和长丝拉伸测量之间存在明显的偏差。我们认为EVF测量的应力太低,特别是在低应变率下,Hoyle等人(2013)也观察到这一点,他们将长丝拉伸测量值与Sentmanat拉伸流变仪测量值进行了比较。因此,对于图3(b)中的ϵ•=0.01 s-1,已经与ϵ•=0.5有偏差,而对于ϵ•=2.5 s-1,EVF测量与DTU-FSR测量一致,最高ϵ•为3.5。请记住,在EVF中,只有横截面的初始面积是已知的;在拉伸过程中横截面面积的变化不是测量的,而是由一个假设均匀单轴拉伸速率不变的方程计算出来的。
此外,在EVF测量中,样品宽度为12.8mm略微超过了Yu等人(2010)建议的12.7mm的上限,这导致在更大的Hencky应变值下的平面延伸而不是单轴延伸。相比之下在DTU-FSR和VADER-1000中,中间直径一直被测量,因此在拉伸过程中横截面的实际面积是已知的,由此计算出中间细丝平面中的真实Hencky应变。
借助于在线控制方案,在整个测量过程中保证了单轴拉伸过程中恒定的Hencky应变率。来自DTU-FSR和VADER-1000的大Hencky应变值的数据由于力小而有些分散。
此外,在拉伸速率超过0.4s-1时,使用DTU-FSR和VADER-1000进行的测量观察到了应力过冲的现象。由于仪器中采用的控制方案的限制,使用两个长丝拉伸流变仪进行测量的拉伸速率不超过2.5s-1。在长丝拉伸中,表面张力可能对测量的应力有影响,尤其是在长丝中间平面的半径非常小,大的亨基应变值的时候。在所有的测量中,最小的半径是R = 0.12mm。如果我们把低密度聚乙烯LDPE的表面张力γ = 0.03 J/m2,表面张力效应产生的最大应力是σsur =γ/R = 250Pa。在图3(b)中,很明显,对于所有达到Hencky应变大于4的测量,测量的应力高于104Pa。因此可以忽略表面张力效应。
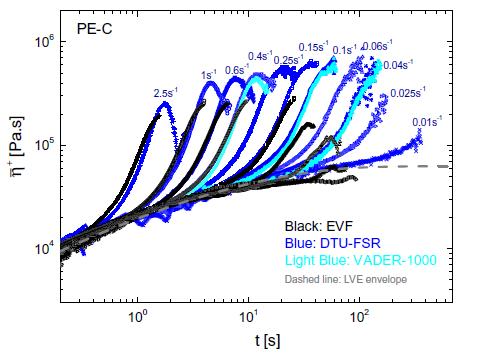
图4
图4显示了PE-C在150℃时拉伸应力增长系数与时间的函数关系。DTU-FSR和VADER-1000的测量结果非常一致。在0.15和2.5s-1之间的中间拉伸速率下,EVF的测量值与DTUFSR一致。拉伸速率低于0.1s-1时,偏差越来越大。根据DTU-FSR和VADER-1000的测量,在拉伸速率快于0.4s-1时,再次观察到应力过冲。
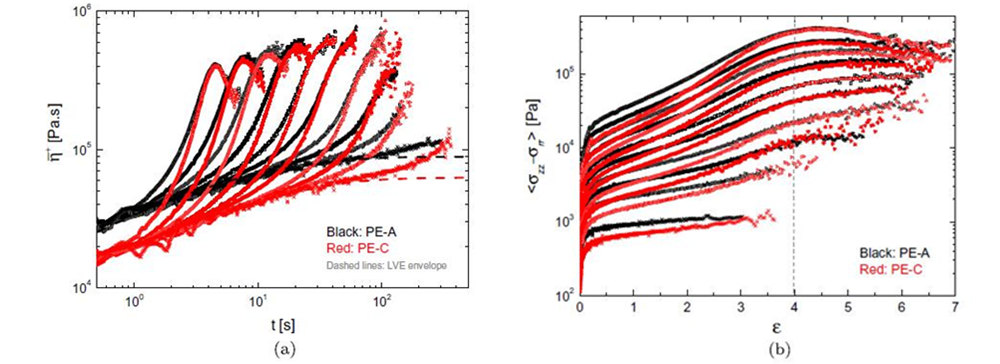
图5
图5比较了DTU-FSR测量的拉伸流动中PE-A和PE-C的非线性行为。如图2所示,PE-A和PE-C具有不同的线性粘弹性,这也由图5(a)中不同的LVE包络表示。在拉伸流的启动过程中,PE-A和PE-C也有不同的非线性反应。从图5a中可以清楚地看出,在所有拉伸速率下,PE-C 比 PE-A 有更明显的应变硬化。然而,在图5(a)、(b)中,有趣的是,尽管PE-A和PE-C最初有不同的非线性行为,但是它们在更大的Hencky应变值下具有相同的反应,并且在每个应变速率达到相同的拉伸稳态粘度,如图6所示。图6还显示在快速应变率下,拉伸稳态粘度表现出幂律行为,粘度比例约为ε•-0.6,这与Rasmussen等人(2005)和Alvarez等人(2013)的观察结果一致。应该注意的是,如图5(b)所示,相同的非线性行为仅在Hencky应变值大于4时观察到,这一点无法通过EVF测量。
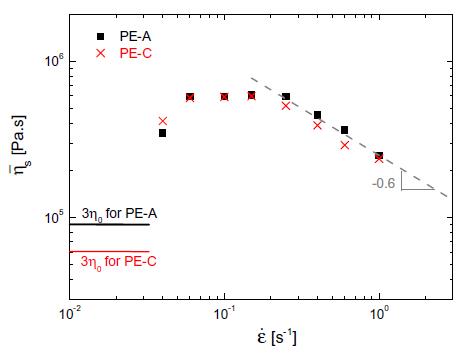
图6
图7(a)比较了PE-B与PE-C在150℃时的拉伸应力增长系数。在所提出的速率下,PE-B没有显示任何应力过冲。尽管PE-B和PE-C在线性和非线性流变学方面的表现不同,但在每种拉伸速率下,它们的相对应变硬化量似乎是相似的。在图7(b)中可以更清楚地看到这一点。图7(b)中比较了Trouton比率。Trouton 比值定义为Tr = η-+ /η0,其中η0是零剪切率粘度,其数值列于表2。可以看出,在每个拉伸速率下,PE-B达到与PE-C相同的最大Trouton比率,证实它们具有相同的相对应变硬化量。
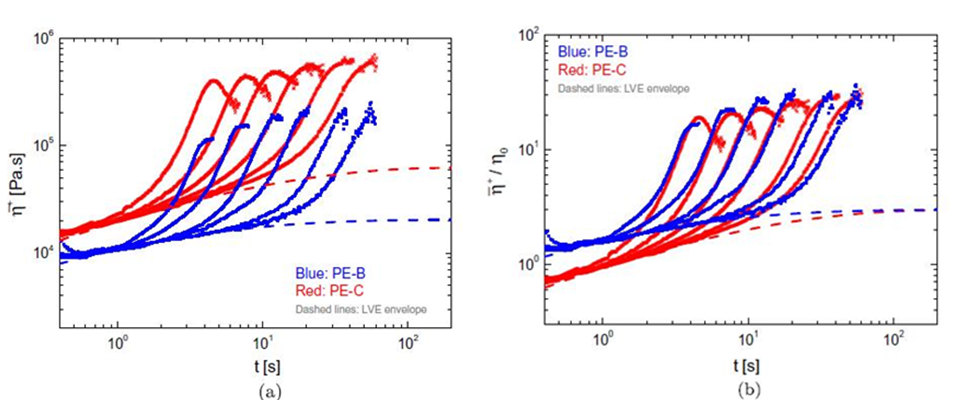
图7
我们使用三种不同的设备测量了三种商用低密度聚乙烯样品的拉伸流变性能。这三种设备在拉伸流变的启动方面给出了一致的结果。然而,EVF的测量结果受到最大Hencky应变4的限制,而两个长丝拉伸流变仪达到了更大的Hencky应变值,在这里可以观察到应力过冲和稳态粘度。此外,EVF的测量仅在取决于应变速率的应变范围内跟随长丝拉伸测量。尽管三种低密度聚乙烯样品具有不同的线性粘弹性能,但已经表明,PE-A和PE-C在Hencky应变值大于4时具有非常相似的非线性rhelogical行为,而PE-B和PE-C具有相同的相对应变硬化量。上述结果表明,工业低密度聚乙烯的非线性流变性可以通过聚合来调整。特别是,有可能合成一种聚合物(PE-C),其具有比参考聚合物(PE-A)低得多的粘弹性模量,但仍具有与参考聚合物相同的拉伸粘度。
原文:A new look at extensional rheology of low-density polyethylene
论文号:Rheol Acta (2016) 55:343–350 DOI 10.1007/s00397-016-0921-z
作者:Qian Huang · Marc Mangnus · Nicolas J. Alvarez · Rudy Koopmans · Ole Hassager